
Next we will explain what monocytes are, their characteristics, origin, functions and much more. It is about the white blood cells that are found in the blood of our body and have extremely important functions that you should know
What are monocytes?
Monocytes are a type of white blood cell also known as a leukocyte. What can measure up to 18 micrometers and are concentrated between 2 and 8% of all leukocytes in the blood.
It is important to note that the mononuclear phagocytic system is made up of circulating monocytes and tissue macrophages, while promonocytes form part of the bone marrow and mature. It is removed to differentiate from the circular monocytes that after about 8 hours migrate to the different tissues and become macrophages.
What are the characteristics of monocytes?
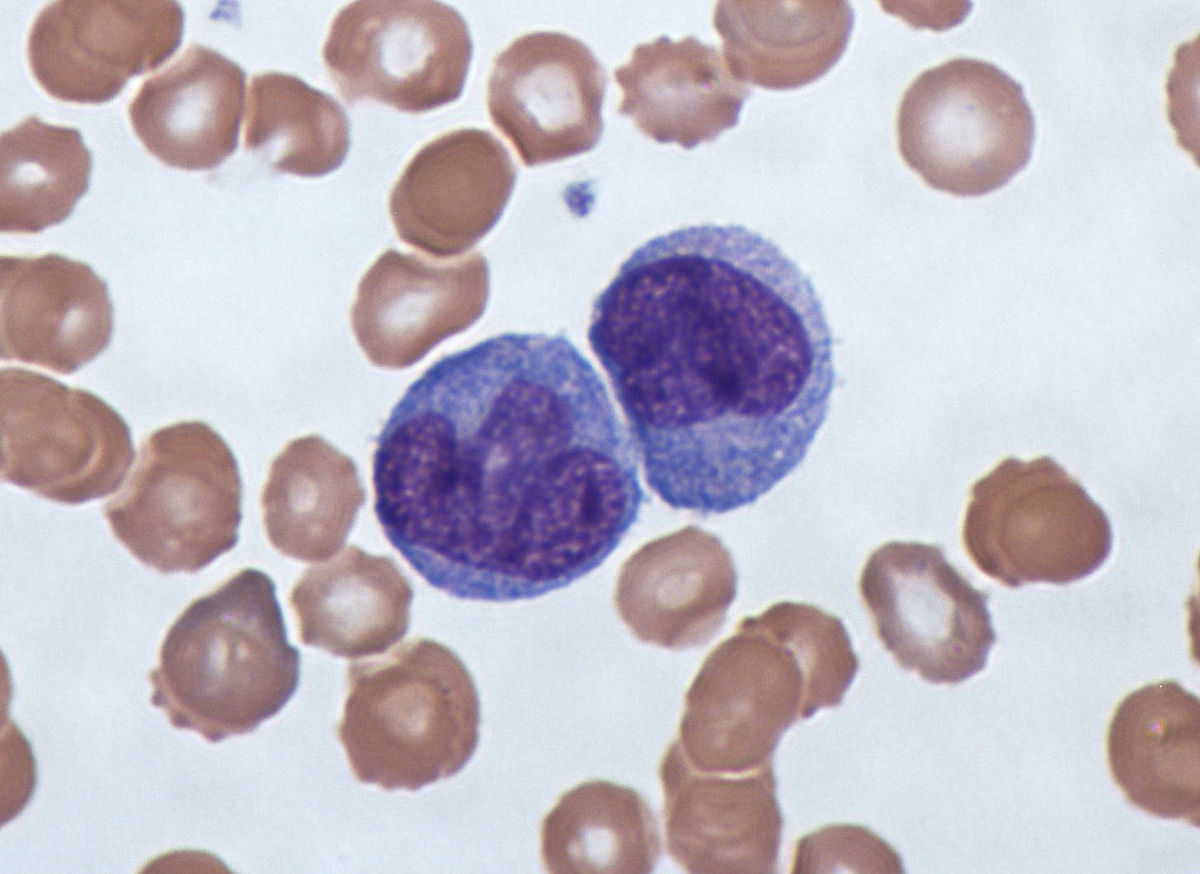
Their most obvious characteristic is that they have a nucleus similar to that of a kidney, lobulated and cerebriform, which is usually irregularly stained with a shape similar to a grid or reticulum of color or Blue or Violet.
Such a nucleus usually contains a 21 ratio to the surrounding cytoplasm and usually has a fairly deep depression. In these cases, the cytoplasm is quite dense and bluish-gray in color, sometimes accompanied by whitish vacuoles.
What is the origin of monocytes?
As we explained before, monocytes are generated in the bone marrow and after a certain time they go to the rest of the tissues through the blood, in this way they reach organs such as the liver, lungs, spleen, lymph nodes, bones and other body cavities.
When they have been in the bloodstream for at least 24 hours, the monocytes leave this current and cross the endothelium of the capillaries towards the connective tissue, where they are easily distinguishable from macrophages.
What are the functions of monocytes?
The main function of monocytes is to eat different microorganisms or cell debris, for which certain factors such as the presence of antigens are taken into account.
Actually, this process is quite simple. It consists of surrounding the pseudopods around the molecule to recognize the cell as a member of a particular tissue of the organism. Through the cmh proteins that exist in cell membranes.
What do high blood monocytes mean?
Monocytes and white blood cells represent a kind of protective shield for the human body, therefore it is essential to maintain their normal values, since any excess or deficit of them implies that their function will be compromised, putting the health of the body at risk.
The main function of monocytes is to eat different microorganisms or cell debris, for which certain factors such as the presence of antigens are taken into account.
When monocytes are elevated, it usually means that the body is suffering from an infection, so it is important. Determine what type of infection and treat it as soon as possible to regulate its functioning.
Normally, monocytes should be between 1 and 8% of the total blood cells which means from 300 to mono hundreds to 900 per liter.
In those cases where the number of monocytes exceeds 900, it means that they are high and timely action is required to return to normal values.
As we mentioned before, the possible causes that cause the elevation of monocytes include hematological inflammatory autoimmune infectious diseases or blood disorders.
There is no particular treatment to lower the amount of monocytes in the blood, but there are specific treatments to attack the disease that is manifesting and thus achieve their natural regulation.
In this sense, it is opportune to go to the doctor to prescribe the corresponding treatment, since this is the professional empowered to indicate the measures to be taken in that case.





